Neural Network: Introduction to Deep Learning

I. From Linear Regression to Neural Network.

Let’s imagine an essential Linear Regression task: House Predicting.

Normally, we could do a Linear Regression, resulting in the following line that barely fits the data.

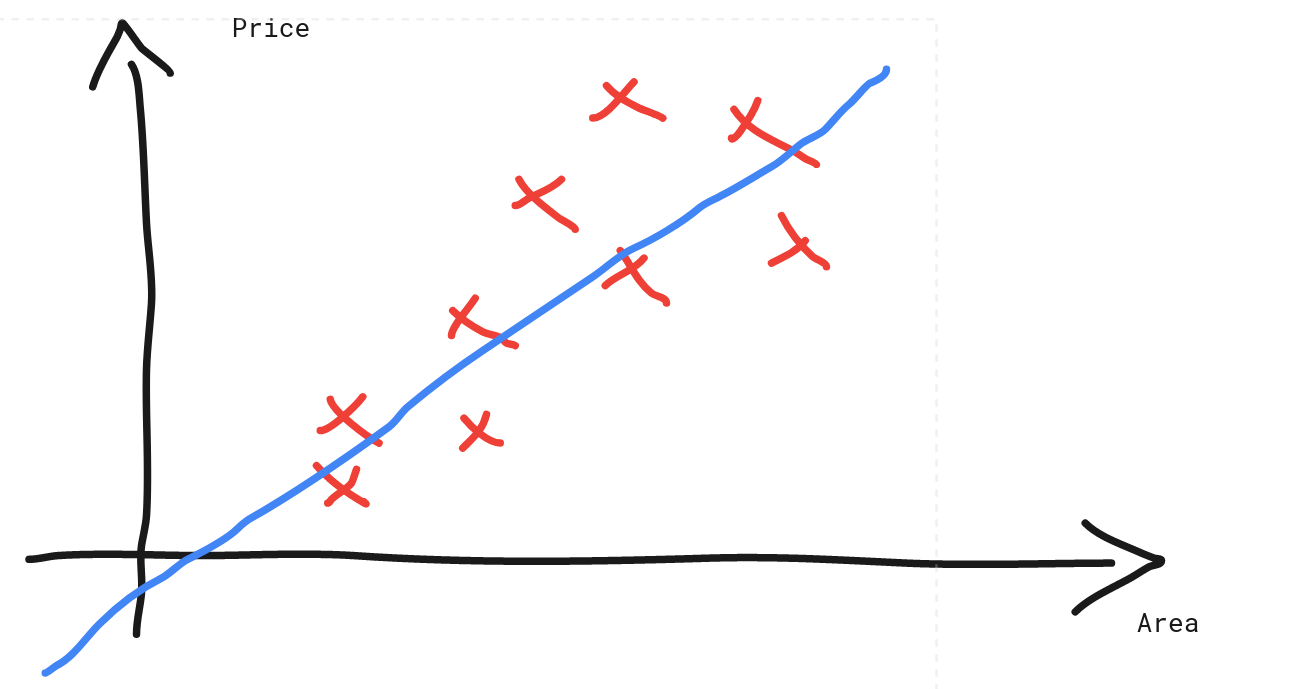
But that raises a new problem, what if the area of the house is low, that is enough to make the prediction $y = \theta x + \beta$ less than zero?

Then, we can have two ways to resolve this problem:

• Use a non-linear model: By adding more features to the model, such as a squared feature or logarithms feature or moreover, combining features by multiplying or dividing (these are feature engineering methods), we can get a model that fits the data better.

For example,

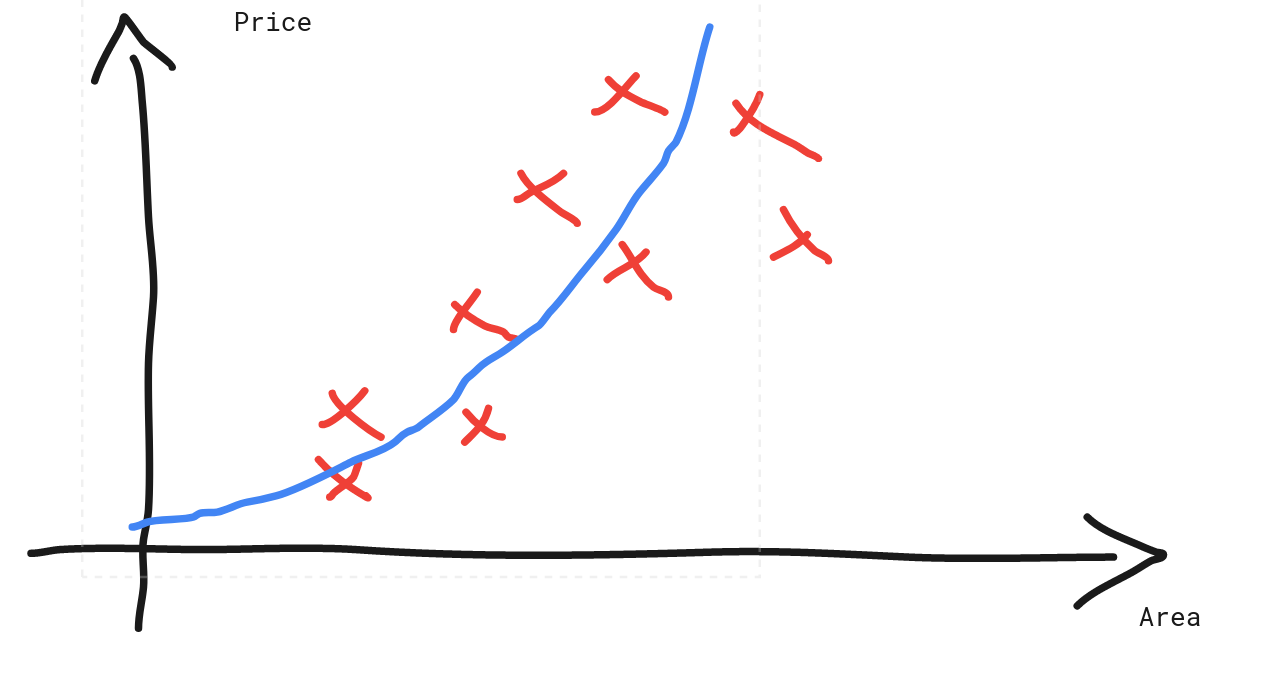
Here, we introduce a new feature, $x^2$ which results in a quadratic model:

$$\theta_{1} x^2 + \theta_2 x + \beta$$

This model fits better than our previous linear model, and it seems that this model’s prediction would not be negative when the $x$ feature is close to zero.

• Use a ReLU model: A simple way to solve this problem is to let the negative prediction be zeroed and keep the prediction if it is positive. And by stating that, we have just defined the ReLU function!

$$y = \begin{cases} x & \text{if } x \gt 0 \\ 0 & \text{if } x \le 0 \end{cases}$$

which created the following model:

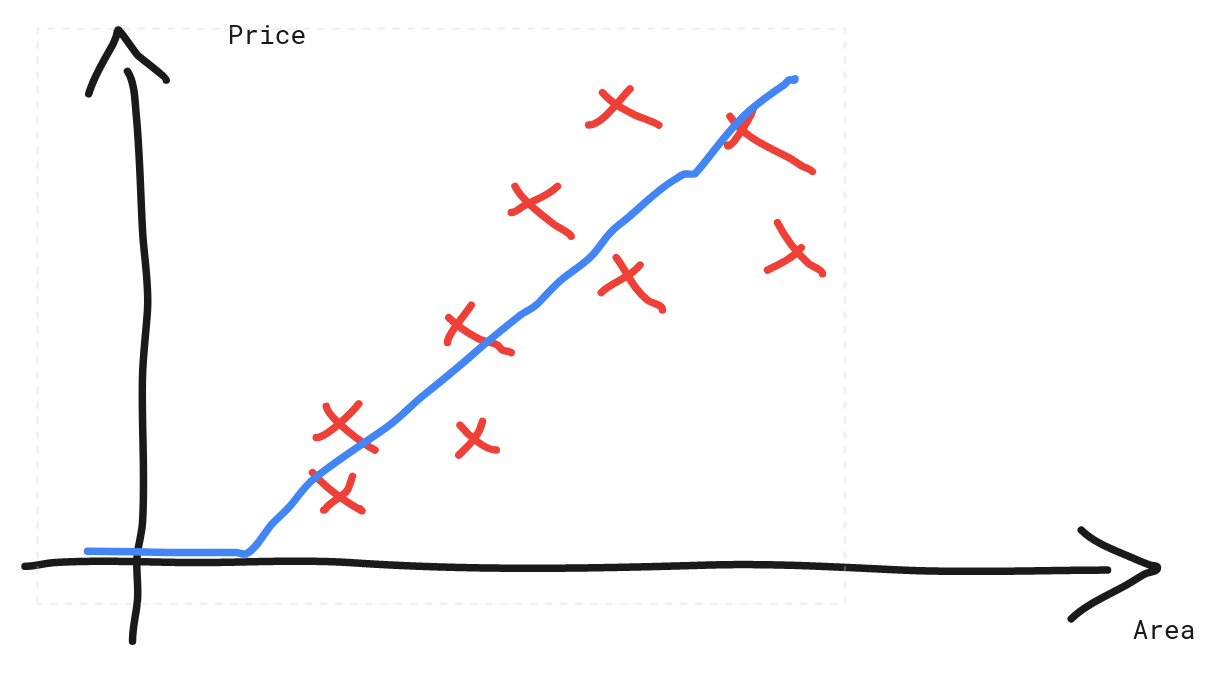
By applying $ReLU(\theta x + \beta)$, we have just created a simple neural network!

II. Basic neural network

You may wonder why the previous example is a simple neural network. Why is it called a neural network?

We can define:

• Node/ Neuron: can be a feature (for input) or the output of a function
• Activation function: a function that defines the output of the node given an input (a node) or a list of inputs (multiple nodes)
• Weights: parameters that transform the input data.
• Bias: is a constant that helps shift the result of the activation function. Therefore, it is critical in Neural Networks

We can now interpret why our model is a simple Neural Network.

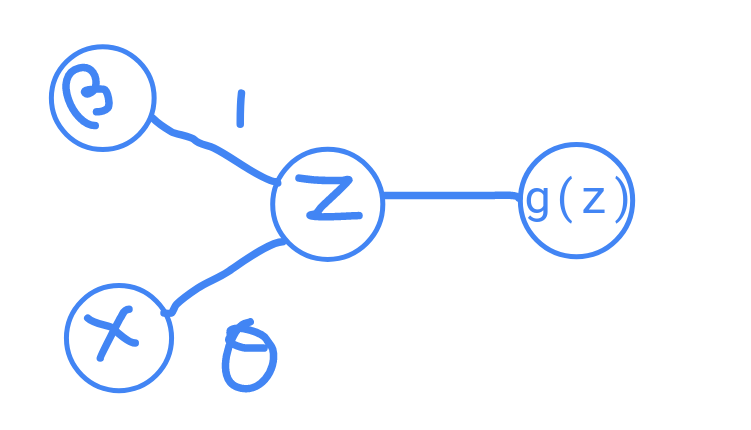
Our feature House Area ($x$) and the bias term ($\beta$) formed two neurons. By multiplying the neurons with their corresponding weights and adding them together $\theta x + \beta$, we get the input for the next neuron. Applying the activation function to the input ($ReLU(\theta x + \beta)$ gives us the next neuron, which is also the output of the model. There are 3 neurons in this model and they form a network, thus the name Neural Network.

We can push ourselves forward by creating a more complicated neural network! Let’s imagine that besides our feature House Area, we are given two more features, Number of rooms and House Age. Then we would go ahead and try a simple Neural Network:

Or we could be more ambitious and create one more layer of neurons:

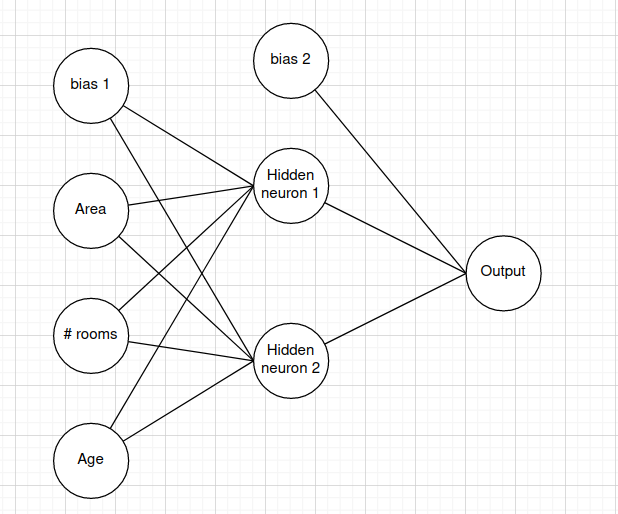
In this neural network, we have multiple layers: an input layer (the first layer), a hidden layer (the middle layer), and the output layer (the last layer). In the input layer, there are 3 features and a bias term, which we define as $x_1$, $x_2$, $x_3$, and $\beta$, respectively. We also defined our weight from the first layer and the second layer as a matrix, where the value of the element at the i-th row and j-th column is the weight of i-th input neuron and j-th neuron in the next layer.

$$W^1 = \begin{bmatrix} w^1_{1,1} & \dots & w^1_{1,j} \\ \cdots & \ddots & \cdots \\ w^1_{i,1} & \dots & w^1_{i,j} \\ \end{bmatrix}$$

Similarly, for the weights between the second layer and the output layer:

$$W^2 = \begin{bmatrix} w^2_{1,1} & \dots & w^2_{1,j} \\ \cdots & \ddots & \cdots \\ w^2_{i,1} & \dots & w^2_{i,j} \\ \end{bmatrix}$$

NOTE: Remember, the bias unit is also a neuron.

You may wonder, what may Hidden Unit 1, and Hidden Unit 2 be? These are the values that the network calculates by itself from the previous layer. Readers may think that these are new features, which are derived from the old ones, that give a better sense to predict the House Price. For example, from the number of rooms and the area of the house, we can know the average area per house, which suggests how large each room is (the larger the room, the more expensive the house is).

So from the start, we get 3 inputs, the Area of the House, the number of rooms, and the age of the house. Then, the model calculates the new features based on these inputs with the corresponding bias unit. After that, it feeds the values of those features to other calculations, with another brand-new bias unit to produce the output of the model. In fact, the current state-in-the-art models are far more complex than the models we have just seen, they can have hundreds of layers, each containing another hundreds or thousands of units!

In fact, in Machine Learning, deriving new features (this is called new neurons in Neural Network) is called Feature Engineering, and the Neural Network has lifted all the hard works for us. But be careful, as this is a tradeoff. Feature Engineering has an inference benefit: one could tell what the new features are about, whereas in Neural Network, we usually have no idea what the new features are!

In conclusion, the next layers’ neurons are just features that are derived from the input’s features. Next time, we will talk about how the network learns using the given set of inputs.